最初，多目标优化问题→通过加权等方式转化为单目标问题→用数学规划求解。

这样每次只能得到一种权值下的最优解。而且MOP的目标函数、约束函数可能是非线性、不可谓、不连续的，传统的数学规划效率低，并且它们对于权值或目标给定的次序比较敏感。

进化算法：通过代与代之间维持由潜在解组成的种群来实现全局搜索。

?

第一代EMO：采用基于非支配排序的个体选择方法和基于适应度共享机制的种群多样性保留策略。代表：NSGA。

? ? ? ? ? ? ? ? ? ? ? ?采用基于非支配排序的思想选择较优个体时需要花费大量的计算量，并且选择效率比较低。

第二代EMO：以精英保留机制为特征。代表：NSGA-II。

? ? ? ? ? ? ? ? ? ? ? ?在求解高维问题时多样性损失严重。

第三代EMO：多种新框架：

1. 基于粒子群优化：PSO
2. 基于免疫算法：NNIA
3. 基于分解：MOEA/D（传统数学规划方法结合进化算法）

?

根据不同的选择机制，EMO分为三类：

1. 基于Pareto支配：NSGA-II、SPEA2
2. 基于指标（比如通过使用HV指标进行选择较优个体保留，较劣个体删除）：IBEA
3. 基于分解：MOEA/D

?

第一代EMO：

• NSGA：非支配解首先被确定。然后被分配一个很大的虚拟适应度值。为了保持种群的多样性,这些非支配解用它们的虚拟适应度值进行共享。这些非支配个体暂时不予考虑。 从余下的种群中确定第2 批非支配个体， 然后它们被分配一个比先前非支配个体共享后最小适应度值还要小的应拟适应度值。这些非支配个体也暂时不予考虑， 从余下的种群中确定第3 批非支配个体。该过程一直持续到整个种群都被划分为若干等级为止NSGA采用比例选择来复制出新一代.NSGA 的计算复杂度为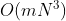，其中声是目标个数万是种群大小.其计算复杂度较高， 而且需要预先确定共享参数。
• NPGA ：设计了基于Pareto支配关系的锦标赛选择机制。具体思想如下：随机地从进化种群中选择两个个体，再随机地从进化群体中选取一个比较集， 如果只有其中1 个个体不受比较集的支配， 则这个个体将被选中进入下一代；当它们全部支配或全部被支配于该比较集时，采用小生境技术实现共享来选取其中之一进入下一代。算法选取共享适应值大的个体进入下一代.该算法中，小生境半径的选取和调整比较困难，还要选择一个合适的比较集的规模。

第一代进化多目标优化算法以基于非支配排序的选择和基于共享函数的多样性保持为其主要特点。在第一代进化多目标优化的发展期间，一些亟需解决的问题也凸显出来。首先， 能否找到替代小生境(共享函数)的方法来保持种群的多样性。适应度共享是针对多峰函数优化提出来的，通常需要关于有限峰数量的先验知识和解空间小生境均匀分布的假设。对于多目标优化问题，同样需要确定共享半径的先验信息，其计算复杂度为种群大小的平方。

?

第二代EMO：

• NSGA-II：是2002年Deb 等人对其算法NSGA的改进，它是迄今为止最优秀的进化多目标优化算法之一。相对于NSGA而言,NSGA-II具有以下优点：① 新的基于分级的快速非支配解排序方法将计算复杂度由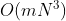降到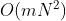，其中，m 表示目标函数的数目、N 表示种群中个体的数目。② 为了标定快速非支配排序后同级中不同元素的适应度值，同时使当前Pareto前沿面中的个体能够扩展到整个Pareto前沿面，并尽可能地均匀遍布。该算法提出了拥挤距离的概念，采用拥挤距离比较算子代替NSGA中的适值度共享方法，拥挤距离的时间复杂度为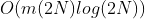。③ 引入了精英保留机制，经选择后参加繁殖的个体所产生的后代与其父代个体共同竞争来产生下一代种群，因此有利于保持优良的个体,提高种群的整体进化水平。

第二代EMO以精英保留策略为主要特征，并且大多数算法不再以适应度共享的小生境技术作为保持种群多样性的手段，一些更好的策略被提出来，比如基于聚类的方法、荃于拥挤距离的方法、墓于空间超格的方法。

?

当前EMO研究热点：

• 基于粒子群优化的多目标优化：PSO是1995年由提出的群智能优化算法,它将种群中每个个体看成搜索空间中的一个没有体积和质量的粒子.这些粒子在搜索空间中以一定的速度飞行,其速度根据其本身的飞行经验和整个种群的飞行经验进行动态调整.优点在于流程简单易实现,算法参数简洁, 无需复杂的调整, 因此, 从提出至今, 已被迅速用于遗传算法原有的一些应用领域.
• 墓于人工免疫系统的多目标优化：是受免疫学启发, 模拟免疫学功能、原理和模型来解决复杂问题的自适应系统, 已被成功用于异常检测、计算机安全、数据挖掘、优化等领域。NNIA模拟了免疫响应中多样性抗体共生 、少数抗体激活的现象, 通过一种基于非支配邻域的个体选择方法, 只选择少数相对孤立的非支配个体作为活性抗体,根据活性抗体的拥挤程度进行比例克隆复制, 对克隆后的抗体群采用了有别于G A 的重组操作和变异操作, 以此加强对当前P aer ot 前沿面中较稀疏区域的搜索. NNIA是一种非常有效的EMO算法。当目标个数达到9 时, 对于较困难的DTLZ 问题,NNIA仍能得到较为令人满意的性能, 显示了该方法在求解高维多目标优化问题时具有很大的优势
• 基于分布估计算法的多目标优化：

• 基于分解的多目标进化算法：将多目标优化问题转换为单目标优化问题是用数学规划方法求解多目标优化问题的基本策略, 典型的转
  换方法包括权重和法、切比雪夫法、边界交叉法等.该算法将通近整个Pareto前沿面的问题分解为一定数量的单目标优化问题,然后用进化算法同时求解这些单目标优化问题. 算法维持一个由每个子问题的当前最优解组成的种群, 子问题之间的近邻关系定义为子问题权重向量之间的距离, 每个子问题的优化过程通过与其近邻子问题之间的进化操作来完成.该算法成功地将数学规划中常用的分解方法引入到进化多目标领域,而且可以直接采用进化算法求解单目标优化问题时的适应度分配和多样性保持策略. 将数学规划方法与进化算法相结合是求解多目标优化问题的一种有效方法, 为进化多目标优化提供了一种新思路。

?

测试问题：

ZDT问题由6 个具有不同性质的两目标优化问题组成, 其PF已知, 是目前采用得最多的测试问题之一。

DTLZ问题能够扩展到任意多个目标, 从而能够很好地扩展为高维多目标优化问题，也是目前采用得最多的测试问题之一。但是，ZDT问题和DTLZ问题也具有明显的缺点，如目标函数缺乏平坦区域、缺少连续空间上的骗问题、PF和定义域空间过于简单等等。

?

指标：